Why Quarto?
There are a few reasons for why I would like to try Quarto (Allaire 2022) as my blogging platform. As I want to write more things of scientific nature I would like to be able to easily cite articles. For example later in this example page I use volume functions from the article Single-tree biomass and stem volume functions for eleven tree species used in Icelandic forestry (Arnór Snorrason and Stefán Freyr Einarsson 2006).
Other reasons are the capabilities of working with the data right in the blogging system and creating the charts and tables in the same area as I write the post.
Working with data
For example we have the following data that I would like to work with.
First I would like to do basic manipulation of the data.
trees$dbh <- (trees$diam1 + trees$diam2) / 2
trees$ba <- (trees$dbh/200)^2 * piFor the next trick we use linear regressions to calculate the expected height of the trees. We then use coalesce() to copy back the height we already knew. From there we can calculate the volume of each tree using the volume functions (Arnór Snorrason and Stefán Freyr Einarsson 2006).
trees$height <- lm(height_measured ~ ba, data=trees) %>%
predict(trees)
trees$height <- coalesce(trees$height_measured, trees$height)
trees$v <- 0.1299 * trees$dbh^1.6834 * trees$height^0.8598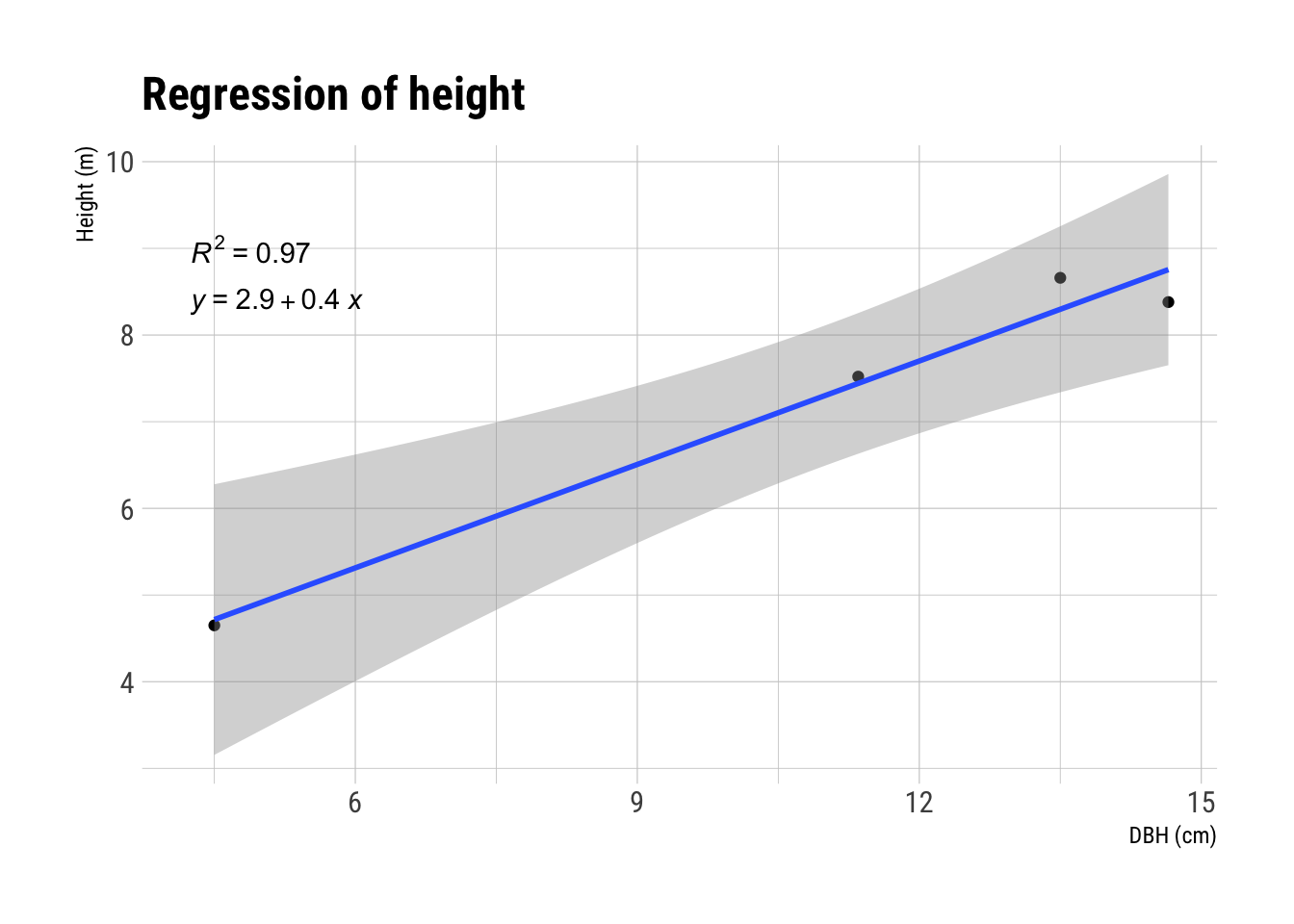
Math with R
Using LaTeX math symbols we can communicate mathematical functions in a nice manner. For example we can talk about BAL as described by Arne Pommerening’s excellent article Basal area in larger trees and the growth compensation point where he explains BAL as such:
BAL is related to available light, since with increasing basal area of larger trees there is less light available for smaller trees. In a sense BAL is a surrogate for light measurements with the benefit that stem diameters and basal area are easier to measure.
\[BAL_i(t) = G(t) \cdot (1 - p_i(t)) \text{ where } p_i(t) = \frac{1}{G(t)} \sum_{\leq g_i(t)} g_i(t)\]
He also give us an example function in R. Let us use it to calculate the BAL of individual trees in our example data.
bal <- function(ba, area) {
sumba <- sum(ba)
basmaller <- 0
pix <- 0
bal <- 0
for (i in 1 : length(ba)) {
bax <- ba[i]
basmaller <- sum(ba[ba <= bax])
pix <- basmaller / sumba
bal[i] <- sumba * (1 - pix) / area
}
return(bal)
}
# An then run it for out 0.54ha example stand.
trees$bal <- bal(trees$ba, 0.54/10000)